1. Introduction

The discrete mountain car is a deterministic environment, where a car is initially placed at the bottom of a sinusoidal valley, and its goal is to reach the flag at the top, as quickly as possible.

2. Environment

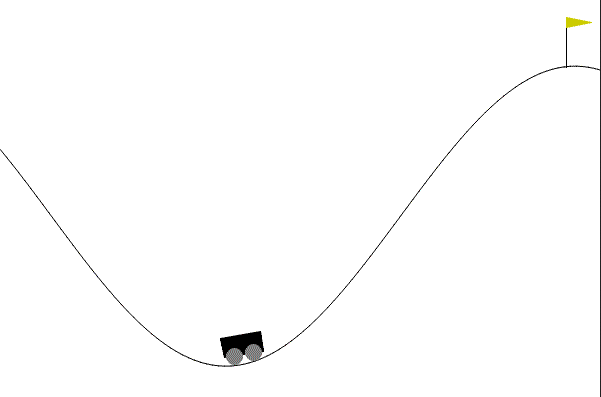
Initial position of the car, and the flag at the top.

Each state is defined by:

Position of the car along the x-axis.
Velocity of the car.

At each time step, the agent can take 3 actions:

Accelerate to the left.
Do nothing.
Accelerate to the right.

Initially, the car is placed at a random point in the x-axis between [-0.6, -0.4], and its velocity is 0.

3. Basic setup

Import and build the environment.

            
env_id = 'MountainCar-v0'
env = gym.make(env_id)

Here are the most important basic functions to call to the environment:

            
# Reset the environment: sets the car's initial position and velocity.
env.reset()
# Render the environment to see it.
env.render()
# Perform an action: accelerate to the left, right, or nothing.
env.step(action)
# Sleep: wait a little bit between actions, to see the car move properly.
time.sleep(0.01)

4. Naive strategies

In this first chapter, I will implement a few simple strategies that require no theory to be coded, just some simple reasoning.

Thereupon, they are generally not sophisticated to achieve a good performance, but they are a good starting point to understand the environment and create a baseline.

The code can be found here. Each implementation explained at the following subsections, has its own class, with a parent class MCDNaive.

4.1 Maximize mean reward

The simplest form of reward function is the mean of rewards generated by the environment.

After around 700 steps, the car overfits learning to gain momentum (Figure 4.1), but it does not take advantage of it, so it ends up only moving backwards to gain as much momentum as possible.

See the source at child class MCDNaiveMean.

4.2 Sin function rewarding

As we know that the hill is a sin function, we can get the corresponding y-axis, also, we know that the higher the car is, either the more momentum it is obtaining or the closer it is to the flag.

Following that reasoning, we define the reward function as:

            
(rewards[curr_state][action] + # Previous reward for selected action.
(gym_reward * \ # Gym reward, penalizing as it is always -1.
(1 / (sin_of_pos * sin_reward_reducing)) * \ # y-axis value ('height').
(1 / (abs(velocity) * velocity_reward_reducing)) * \ # current velocity.
(1 / (abs(env_high - pos) * flag_distance_mult)))) \  # distance to flag.
/ 2 # Average.

Where 4 new variables are defined:

sin_of_pos = sin(pos)
sin_reward_reducing: to control the weight of the y-axis value. Inversely proportional.
velocity_reward_reducing: to control the weight of the velocity. Inversely proportional.
flag_distance_mult: to control the weight of the distance to the flag. Directly proportional.

As seen in Figure 4.2, the car, starting from -0.4177 is able to reach the flag in 2075 steps, taking 54 seconds to do so. Thus, it will be used as baseline.

See the source at child class MCDNaiveSin.

Discrete mountain car

Abstract