Abstract

Humans partly learn by observing, trying, failing and retrying in order to achieve their goal. That's the main idea behind reinforcement learning. In the present page, the basic setup and concepts of this type of machine learning are exposed, as well as a brief overview of methods.

1. Introduction

Reinforcement learning is a branch of machine learning, that deals with how to learn control strategies to optimally interact with an environment from experience.

This biologically inspired idea, sets an interactive framework that then proposes an optimization problem, both of which we'll inspect next.

2. Components and workflow

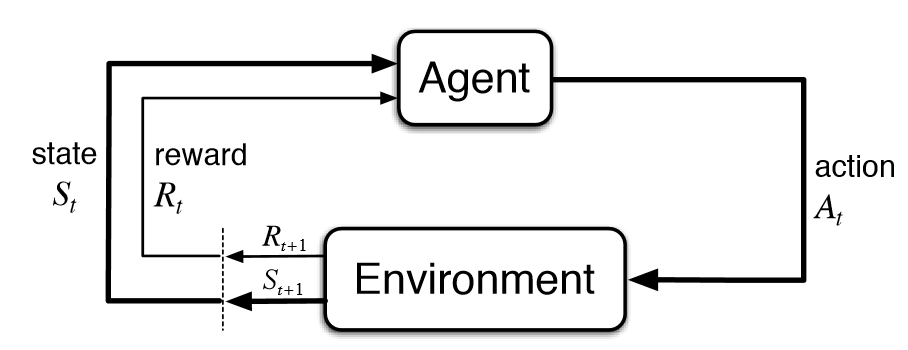
Figure 1.1: Reinforcement learning workflow. Source: Towards Data Science.

As seen in Figure 1.1, the workflow is as follows:

At a given time t, the Agent is observing the State for that time step.
The Agent interacts with the Environment by carrying out an action A at time step t.
The Action, may or may not change the Environment. Depending on its consequences, the Agent will get a concrete reward, and the state that it can observe, will transition to the one corresponding to the next time step.
If no termination state is reached, the process continues from 1. Else, it ends.

Now that we've seen the workflow, let's define more in depth each of the components.

Agent

The agent is the entity that interacts with the environment. It is the one that carries out the actions, and observes the state of the environment. It is also the one that learns from the environment, and tries to optimize its actions.

There may be one or more agents in the environment.

Environment

The environment is the entity that the agent interacts with. It is the one that changes its state depending on the actions of the agent, and gives rewards to the agent.

Depending on the different variables examined in it, they can be:

Variable	Type 1	Type 2
Agent's observability	`Fully observable`	`Partially observable`
State transitioning	`Deterministic`	`Stochastic`
Number of actions	`Discrete`	`Continuous`
Actions correlation	`Episodic`	`Non episodic`
Number of agents	`Single agent`	`Multi-agent`
Changes with time	`Static`	`Dynamic`
Multi-agent relations	`Competitive`	`Collaborative`

State

The state is the representation of the environment at a given time step. It is the one that the agent observes at each time step separately, and that the environment changes depending on the actions of the agent.

Each state can be either:

Fully observable: The agent can observe all the information about the state.
Partially observable: The agent can only observe a subset of the information about the state.

Action

The action is the entity that the agent carries out at each time step. It is the one that changes the state of the environment, and that the environment rewards or punishes the agent for.

Reward

The reward is the entity that the environment gives to the agent at each time step. It is the one that the agent tries to maximize, and that the agent learns from.

The reward can be either:

Immediate: The reward is given at the same time step that the action is carried out, which would be a fully supervised learning approach, except for the fact that there is no actual dataset with target labels for each sample before beginning to solve the optimization problem.
Delayed: The reward is given at a later time step. In this case, we would categorize the learning method as semi-supervised.

4. Behind the scenes

The goal of reinforcement learning is to design an optimal probabilistic policy function $π (s, a)$ for deciding which actions to take given a state to maximize the future reward.

That means we aim to generate the most optimal sequence (denominated as trajectory or episode) of time contiguous [state, action, reward] tuples of the form:

τ = (S_{0}, A_{0}, R_{0}, S_{1}, A_{1}, R_{1}, ..., S_{t - 1}, A_{t - 1}, R_{t - 1}, S_{t}, A_{t}, R_{t})

To start, the state $S_{0}$ is randomly sampled from the start-state distribution, $ρ_{0}$ , in which $S_{0} ~ ρ_{0} (\cdot)$ .

Transitions between states may be:

Deterministic: for the same state $S_{t}$ and action $A_{t}$ , the resulting state $S_{t + 1}$ obtained from the computation of the function $f (S_{t}, A_{t})$ , never varies.
Stochastic: instead of a function, the next state is sampled from a probability distribution.
$S_{t + 1} ~ ρ (S_{t + 1} ∣ S_{t}, A_{t})$

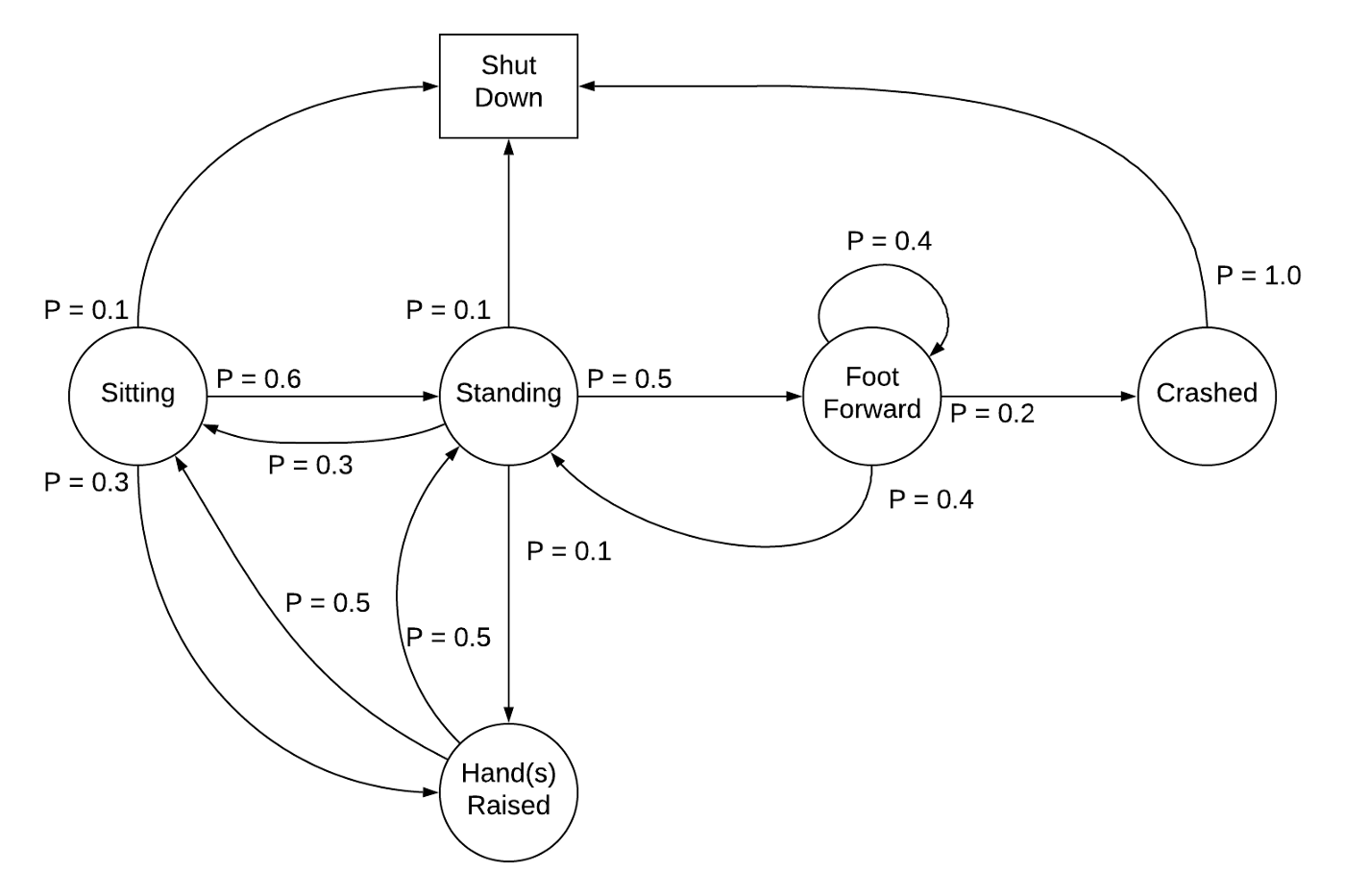
The mentioned trajectories, are possible because the agent is describing a Markov Decision Process (see Figure 4.1), which itself is an extension of Markov chains. It exhibits the Markov (memoryless) property, as probabilities of different outcomes are not dependent on the whole past history, just the previous state and action. In order to find the optimal trajectory, we can follow

Figure 4.1: Example of a Markov Decision Process. Source: Towards Data Science.

For achieving the previously mentioned goal, there are two different strategies.

Value learning

Tries to quantify the value (expected return) of each state-action pair which can be obtained following a policy

π

V_{π} (s) = 𝔼_{π} {R_{t} ∣ s_{0} = s}

= 𝔼_{π} {\sum_{t} γ^{t} r_{t} ∣ s_{0} = s}

= 𝔼_{π} {r_{0} + \sum_{t = 1}^{\infty} γ^{t} r_{t} ∣ s_{1} = s^{'}}

= 𝔼_{π} {r_{0} + γ V (s^{'})}

for every time step

t

When maximized over all possible policies, it conforms the Bellman Equation,

V (s) = max_{π} E {r_{0} + γ V (s^{'})}

which if satisfied, means that the problems it is being applied to exhibits an optimal substructure, hence, it can be solved by using dynamic programming.

It is important to note that $γ ϵ [0, 1]$ represents a constant, called the discount rate, which makes more worthy the rewards obtained during the first actions. This is used for both episodic and continuing tasks, so that the sum of future rewards always converges. When it is equal to one, the agent is said to be far sighted, while on the other hand, when it is equal to zero, the agent is said to be myopic. In practice, it is often set to a value between 0.95 and 0.99.

From a human learning point of view, this methodology is closer to how a baby learns new concepts, by exploring and experimenting, not trying to find a previously known optimal path to the solution.

Policy learning

Policy learning focuses on directly inferring a policy that maximizes the reward on a specific environment. Therefore, a mapping from states to action is kept in memory during learning. While a value function may be used to optimize the policy parameters, it won't be used to select an action.

The final goal, as said before, is to find the optimal policy, $π_{*}$ , which maximizes the total return.

5. Useful resources

Reinforcement Learning: Machine Learning Meets Control Theory, by Steve Brunton.
DeepMind x UCL RL Lecture Series, by DeepMind.